Notatki z pliku notes/mikro/mikro_0000.00.00.md
Podstawy Mikroelektroniki¶
Notatki z pliku notes/mikro/mikro_2025.10.01.md
Laby¶
Intro¶
pierwszy tranzystor ostrzowy
pierwsze tranzystory złączowe
pierwszy układ scalony
powstanie technologii CMOS (Complementary Metal-Oxide Semiconductor) (tranzystor polowy)
Informacja
w dzisiejszych czasach zasßpeuje się rezystory i kondensatory tranzystorami, bo tranzystory są najmniejsze i najtańsze.
Parametry tranzystora¶
Przy produkcji ukłądów scalonych określa się parametr \(L_{min}\) czyli najniższa szerokość kanału.
Notatki z pliku notes/mikro/mikro_2025.10.08.md
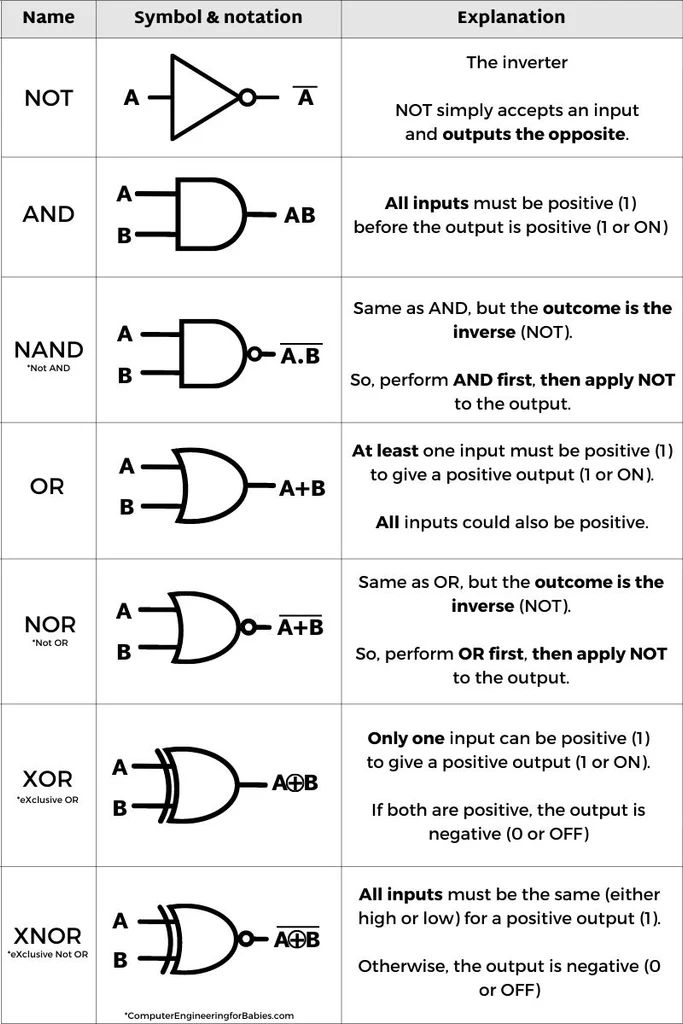
Logika cyfrowa¶
Wyróżniamy 2 stany logiczne: 0 (napięcie GND) oraz 1 (napięcie zasilania).
Algebra Boole’a¶
Operacje elementarne:
negacja \(\bar{x}\)
\(a + b\) (OR)
\(a \cdot b\) (AND)
podstawowe własności:
\(a*b = b*a\) (przemienność) [dualizm] \(\Leftrightarrow a + b = b + a\)
\((a*b)*c = a*(b*c)\) (łączność)
Do opisu ukłądów logicznych używa się “tablicy prawdy” lub funkcji logicznych.
Minimalizacja funkcji logicznych - Tablice Karnough¶
\(x_2 ~ x_1 x_0\) |
00 |
01 |
11 |
10 |
|---|---|---|---|---|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
Wskazówka
w pierwszym wierszu jest tzw. kod Gray’a
Teraz szukamy prostokątów o bogu \(2^n\) (tabelka się loopuje). i zapisujemy sumę iloczynów albo i9loczyn sum
Notatki z pliku notes/mikro/mikro_wyklad_yt.md
Notatki z wykładu na youtube¶
https://www.youtube.com/watch?v=yQDfVJzEymI&list=PLyYrySVqmyVPzvVlPW-TTzHhNWg1J_0LU
Półprzewodniki¶
Istnieją 2 sposoby przenoszenia ładunków w półprzewodniku:
elektrony
dziury
Ważne
Przenoszenie poprzez dziury jest wolniejsze niż poprzez elektrony gdyż technicznie wymaga ono uwolnienia elektronu z jednego wiązania i wychwyt przez wiązanie “z dziurom”
Definicja eV
Elektroo-volt, to ilość energii potrzebnej, aby przetransportować jeden elektron przez różnicę potencjałów jednego volta.
Wzór na ilość wolnych elektronów w półprzewodniku:
Gdzie:
\(T\) - temperatura bezwzględna
\(E_g\) - przerwa energetyczna
\(E_g\) [eV] |
Atom |
|---|---|
0.67 |
German |
1.12 |
Krzem |
2.5 |
Diament |
Informacja
Wiemy, że diament jest izolatorem, dlatego jego energia jest tak duża.
Wskazówka
Wiemy, że dla krzemu \(n_i \approx 10^{10}\)
Oznaczmy:
\(n\) - koncentracja (liczba / gęstość) wolnych elektronów
\(p\) - koncentracja dziur
Wskazówka
Dla krzemu niedomieszkowanego (czystego) \(n = p = n_i\)
Domieszkowanie pozwala nam zwiększyć liczbę elektronów/dziur w półprzewodniku. Domieszkujemy atomy z 5 lub 3 elektronami walencyjnymi.
Przykładowo, gdy chcemy zwiększyć liczbę elektronów, dodajemy atomy fosforu w liczbie \(N_D\) (donorów) (zazwyczaj między \(10^{15}\) a \(10^{17} \frac{atom}{cm^3}\) atomów). Jak widać, liczba domieszkowanych atomów znacząco przeayższa liczbę wolnych elektronów natywnie w krzemie \(\Rightarrow n \approx N_D\). Można także stwierdzić, że:
Domieszkowanie¶
https://www.youtube.com/watch?v=NWolpDgi6_Y&list=PLyYrySVqmyVPzvVlPW-TTzHhNWg1J_0LU&index=2
Gdy dodajemy \(N_D\) atomów donorowych (np. fosforu) na \(cm^3\), przyjmójemy że w materiale będziemy mieć \(N_D\) wolnych nośników (tu elektronów).
Wskazówka
Zakładamy, że \(N_D \gg n_i\)
Wyróżniamy 2 typy domieszkowania:
materiał typu n (donor) - więcej elektronów
materiał typu p (akceptor) - więcej dziur
Przepływ nośników¶
Dryf to przepływ ładunków spowodowany różnicą potencjałów (polem elektrycznym).
Taki przepływ określa prawo Ohma \(U = I\cdot R\). Jednak jak znaleźć R?